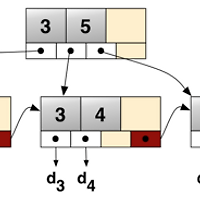
정확히는 해싱(해슁)에 관한 글이지만 연장/확장 해쉬에 관한 개념을 잡기 위하여.
I. 해슁의 개요
가. 해슁의 정의
- 여러개의 명칭(identifier)들이 무작위로 들어있는 테이블에서 특정 명칭을 찾고자 하는 경우
- Hashing 은 키 값에서 레코드가 저장되어 있는 주소를 직접 계산한 후 산출된 주소로 곧바로
접근이 가능하게 하는 방법.
- 검색할 때 키 값을 비교하는 것이 아니라 계수적 성질을 이용, 계산에 의하여 주소를 결정하여
기억 공간에 레코드를 보관하거나 검색하는 방법
나. 해슁의 주요 개념
- 해쉬 함수(hash function) : 원하는 키값을 가지는 테이블 항목을 검색하기 위해 특정한 변환 함수
를 이용하여 키값을 항목 의 주소로 직접 바꿔서 검색하는 방법을 해슁이라 한다. 이때 사용하는 변
환 함수를 지칭.
- 해쉬파일: 해슁함수를 이용하여 레코드의 키 값을 물리적 레코드의 주소를 계산해 레코드를 저장,
검색하는 파일
- 홈주소 : 해싱함수에 의해 계산된 번지로 자료가 저장되는 주소 .
- 해쉬 테이블 (hash table) :해싱함수에 의해 산출된 함수값 홈주소 의 위치에 해당 자료를 기억시킨
해시표 . 일반적으로 배열로 선언되고 배열은 bucket 과 slot 으로 구성됨 . ,
=> 명칭 테이블의 기억공간 낭비를 막기 위해 해쉬 테이블을 사용.
=> 해쉬 테이블은 b개의 버켓(bucket)으로 구성되고, 하나의 버켓은 s개의 슬롯(slot)으로 구성.
=> 각각의 슬롯에는 명칭 테이블 항목처럼 하나의 명칭이 저장.
-버킷: 키의 주소에 따라 어떤 종류의 데이터들이 기억될 공간
=> 해싱함수로 계산된 값에 데이터를 기억시키기 위한 기억 장소로서 해싱 기법에서 볼 때 동일한 하나의 주소를 가지는 파일의 한 구역
다. 해슁의 필요성
- 명칭 테이블에서 키 값과 일치하는 명칭을 찾는 방법으로는 테이블에 있는 각각의 명칭을 키 값과
차례로 비교하는 방법이 있다.
- 이 방법을 사용하면 최악의 경우 n회의 비교가 필요하다. 해슁을 이용하면 해쉬 함수가 킷값을
해당 주소로 단번에 변환해 주므로 매우 빠른 검색이 가능하다.
라. 해쉬파일의 특징
-주소공간에 대한 논리적 물리적 독립성 유지 ,
- 키에 대응하는 Hash 값에 맞는 Bucket에 데이터를 저장
- Direct File 이라 함은 보통 Hashed File 을 의미
-삽입 삭제가 용이함
-빠르고 일정한 검색속도를 가지는 장점이 있음
-키 변환 방법에 따라 공백이 많이 생기므로 기억공간 사용 효율성 低
-연속적인 일괄처리는 비효율적임
마. Hashing 의 장점 및 단점
|
장점 |
검색 방법 중 속도가 가장 빠름. 각각의 레코드를 비교해 찾는 번거로움을 피할 수 있음. 이진 탐색보다 조금 많은 기억 장소를 차지하나 기억 공간이나 속도면에서 우수. Overflow 가 없으면 한번에 원하는 레코드에 접근. ISAM보다 세 배나 빠른 검색 속도를 지니고 있다. 데이타에 대한 입력이나 삭제가 쉽다. 검색 시간(retrieval time)이 데이타의 양과 상관없이 일정하게 유지된다 |
|
단점 |
연속적인 데이터 검색에는 비효율적이다. 디스크 공간이 비효율적으로 사용된다 정형 해슁의 경우, 데이터가 꽉 차서 디스크 공간을 늘리고 재구조화를 하게 되면, O(n)번에 해당하는 디스크 검색을 해야 하므로 시간이 많이 걸리게 된다. Collision 현상이 많이 생길 경우 Overflow 처리가 많아지고, 기억 장소가 낭비됨 모든 데이터를 수치 형태로 바꾸어야 함. 적당한 해싱 함수 선정에 문제가 있음. 기억 공간 할당 크기를 알 수 없으므로 해쉬표를 위한 기억장소 할당의 어려움. |
바. 해슁(Hashing)과 데이터베이스(Database)
검색 속도가 아무리 빠른 해슁을 이용할 지라도 디스크의 검색 속도가 느리다면, 해슁의 장점은 무용지물이 되며, 아무리 좋은 디스크를 가지고 있다 하더라도, 해슁의 검색 속도가 느리게 되면, 이 디스크는 그 가격 만큼의 성능을 발휘하지 못하게 되는 것이다. 따라서 해슁에서는 디스크 속도와 균형을 이루는 것이 중요하다. 이것이 해슁의 데이타베이스적 접근이다
II. Hashing 구현기법
가. 정적 해슁
1) 정의
- 정적 해슁은 고정 크기의 테이블을 이용하여 해슁하는 방법으로서 한번 저장된 명칭의 상대적
위치가 변경되지 않는다.
- 버켓 주소의 집합을 고정시키는 것 .
- 고정된 Bucket을 미리 할당하는 방법
2) 특징
- 현재 파일 크기에 근거하여 해싱함수 선택
- 미래의 어떤 시점의 파일 크기를 예상하여 해싱함수 선택 초기 많은 양의 저장공간 낭비
- 파일의 크기가 커짐에 따라 주기적으로 해싱 구조 재구성 필요
- 로직이 간단함
- Bucket을 작게 잡을 경우 충돌의 우려가 있으며, 너무 크게 잡을 경우 메모리 또는 디스크 낭비의 우려가 있음
- 데이터 증감에 따른 Hashing 재구조화에 많은 리소스 필요
- 데이터의 증가에 따라 검색성능이 감소함
나. 동적 Hashing 기법 .
1) 정의
-데이터베이스가 확장 또는 축소되는 데에 맞추어 해싱테이블을 동적으로 변경시키는 해싱기법 .
-레코드를 저장하는 버켓 수를 고정하지 않고 필요할 때 늘이거나 줄임.
◇ Hashing 값을 인덱스로 사용하는 이진 트리를 동적으로 변환하여 사용
◇ 버킷을 포인터로 가리키는 버킷 주소 테이블을 생성/유지
◇ 데이터의 증감에 따라 Bucket을 쪼개거나 합치는 과정을 반복
◇ 동적으로 변하는 다중 레벨 인덱스를 관리
2)특징
◇ 로직이 복잡
◇ 버킷 주소 테이블을 생성/유지해야만 함
◇ 데이터가 증가하여도 검색의 성능이 유지됨
◇ 메모리 또는 디스크의 낭비를 줄일 수 있음
-저장공간의 효율성 유지 .
- 데이타의 수가 증가해도, 데이타베이스의 성능이 감소되지 않는다.
- 연결이나 링크(link)와 같은 것이 동적 해슁에는 사용되지 않기 때문에 접근시간(access time)을
일정하게 유지
- 버킷 주소 테이블을 생성해야 하는 부담이 있다
-버켓의 분리와 융합은 다소 부가노력이 필요하므로 성능이 저하됨 .
- 버킷을 직접적으로 검색하기 보다는 버킷 주소을 통해 간접적으로 검색하는 것이므로 추가적인
검색 횟수가 필요하다
- 버킷 주소 테이블을 두 배로 재구조화하는 작업은 시간이 매우 많이 소요되는 작업이다
- 가득찬 버켓에 새로운 레코드가 삽입되면 그 버켓을 두 개의 버켓으로 분할함.
- 분할하는 방법은 해시 값의 다음 유효 비트가 0 인 레코드를 한 버켓에, 1 인 레코드를 또 다른
버켓에 나누어 저장함.
- 디렉토리는 각 버켓에 대응하는 비트 열 형태를 구분할 수 있도록 이진 트리 형태로 구성함.
즉, 레벨 i 에 있는 노드는 해시 값의 i 번째 비트가 0 에 해당하는 왼쪽 포인터와 1 에 해당하는
오른쪽 포인터를 갖음. 단, 리프 노드는 데이터 레코드를 저장하는 버켓의 주소를 갖음.
- 한 레코드를 탐색하고자 할 경우, 그 레코드의 해시 필드 값에 대한 해시 함수 결과 (이진
비트열)을 얻고 이를 기준으로 디렉토리를 탐색하여 버켓 주소를 얻음.
다. 확장 해슁(extendible Hashing)
○ 동작원리
◇ 동적 Hashing 기법에서 가장 많이 사용하는 방법으로 트리의 깊이가 2인 특별한 경우
◇ 사용할 수 있는 비트열을 모두 사용하지 않고 일부 비트열만 사용한 후 더 많은 버킷이 필요할 경우 비트열을 하나 씩 추가
○ 장/단점
◇ 버킷을 쪼개고 합치는 재구조화가 한 번에 하나의 버킷에서만 일어나는 장점이 있음
◇ 현재 필요치 않는 버킷을 절약할 수 있음
○ 특징
- 확장 해슁(extendible hashing)은 동적 해슁에서 가장 많이 사용하는 방식으로 트리의 깊이가 2인 특별한 경우
- 일반적인 동적 해슁의 경우에는 버킷를 쪼개고 합치는 재구조화가 일어날 때, 성능을 낮추는 부하가 발생한다. 그러나 확장 해슁은 재구조화가 한번에 한 버킷에만 발생되므로 상대적으로 부하를 크게 줄일 수가 있게 된다
- 디렉토리는 2d 개의 버켓 주소를 갖는 배열임. 이때 d 는 전역 깊이라 하며, 해시 값의 처음 d 개
비트를 디렉토리 배열의 인덱스 값을 결정하는데 사용함.
- 2d 개 디렉토리 엔트리들은 서로 다른 버켓 주소를 유지할 필요는 없음.
- 처음 d'개의 비트 값이 갖는 레코드가 하나의 버켓에 저장될 수 있으면 여러 디렉토리 엔트리가
같은 버켓 주소를 유지하며, 각 버켓내의 레코드가 기반으로 하는 비트 수 d'을 지역 깊이라 함.
- 지역 깊이 d'과 전역 깊이 d 가 같은 버켓에서 오버플로우가 발생할 경우, 디렉토리 배열 내의 엔트리 수는 2 배가 됨.
- 어떤 레코드를 삭제한 후, 모든 버켓에 대해 d > d' 인 경우 디렉토리 배열내의 엔트리 수는 절반이 됨.
- 대부분의 레코드 검색은 두 개의 블록 접근(디렉토리에 대한 블록 접근, 버켓에 대한 블록 접근)을 필요로 함.
III. 해슁함수
-입력된 키값을 해쉬 테이블의 주소로 변환시켜주는 함수
가. 좋은 Hashing 함수의 조건 .
-키값 분포가 균등 - (uniform)
-버켓은 모든 가능한 탐색 키 값의 집합으로부터 같은 수의 탐색 킷값을 지정 받음 .
-가능한 충돌이 적게 발생해야 함
-계산이 쉽고 빠르게 이루어져야 함
1). Digit analysis 법 (계수 숫자 분석법)
-키를 숫자로 변환하여 표현되는 스트링. (Digit string) 에서 특정 칼럼의 숫자만을 추출하여
홈주소로 사용하는 방법
-키 특성이나 분포가 미리 잘 알려져 있을 때 유용 .
|
key |
홈주소 |
|
0545-984-1604 |
914 |
|
0545-837-5418 |
858 |
2) mid-square 함수(중위 중간제곱법)
- 키 값을 제곱한 후에 중간에 몇 비트를 취해서 해쉬 테이블의 버켓 주소로 변환.
- 키 값을 제곱하면 결과값의 중간 비트들은 키 값의 모든 비트들로부터 영향을 받으므로
버켓 주소가 고르게 분산될 가능성이 높다.
-키값을 제공하여 그 수의 중간 일부분을 추출하여 홈주소로 사용 .
-키값이 상하위자리에 여러개의 0이 연속되어 있지 않은 경우에 사용할 수 있음 .
|
K |
|
홈주소 |
|
524 |
274576 |
45 |
|
714 |
509796 |
97 |
3) division 함수
- 키 값을 해쉬 테이블의 크기로 나누어서 그 나머지를 버켓 주소로 변환.
- 버켓 주소 = 키 값 % 해쉬 테이블 크기
-bucket 의크기에 근접하는 수로 킷값을 나눈 나머지를 홈주소로 사용 .
-나누는 수 선택에 많은 영향 받음 . M(31)
-M은 소수이면서 bucket 크기보다 약간 작은 값일 때 충돌 줄어듬 .
|
key |
홈주소 |
|
357 |
357 % 31 = 16 |
|
124 |
124 % 31 = 0 |
4) folding 함수
- 키 값을 버켓 주소 크기만큼의 비트수를 가지는 부분으로 분할한 후, 분할된 것을 합산하여 버켓 주소로 변환.
-키값을 2개 이상으로 나누어 각 부분을 독립된 수로 간주하여 덧셈한 결과를 홈주소로 함 .
-키필드길이가 매우 길 때 사용 .
Ⅳ Hashing File의 문제점 및 해결방안 .
가. 해슁의 문제점
1). 충돌(collision) 발생 : 서로 다른 두개 이상의 명칭이 해쉬 함수에 의해 동일한 주소로 변환
복수개의 들이 같은 데이터 영역으로 되는 것 key hasing
- 충돌이 자주 발생하면 탐색 시간이 길어지는 등 성능이 저하되므로 해쉬 함수를 수정하거나
해쉬 테이블의 크기를 적절히 조절해 주어야 함.
- 충돌이 발생한 경우 같은 버켓에 있는 다른 슬롯에 명칭을 저장하면 된다.
2). 오버플로우(overflow) : 데이터영역이 꽉 차서 더 이상 데이터를 넣을 수 없음에도 불구하고 다른 키가 그쪽으로 hashing 되는 것
그러나 슬롯의 갯수만큼 충돌이 생기면 빈 슬롯이 소진되어 오버플로우(overflow)가 생길 수 있다. 오버 플로우가 발생하면 해슁에 의해 원하는 명칭을 찾을 수 없게 되므로, 오버 플로우를 해결하기 위한 방법이 고안되어야 한다.
나. 오버 플로우의 해결방법
가). 선형 개방 주소 지정법 (open addressing)
- 충돌이 발생한 경우에 그 위치로부터 비어있는 다른 버켓을 찾아 그곳에 명칭을 저장하는 방법
- 선형 탐색법(linear probing)이라고도 불림.
- 선형 개방 주소지정법을 이용할 때 해쉬 테이블은 1차원 배열 형태를 가짐.
-오버플로우 가 발생했을 경우 다른 데이터 주소를 탐색해서 그곳에 데이터를 넣을 수
있는가를 조사하고 그러하지 못한 경우는 그런 영역을 찾을 때까지 반복해서 수행 ,
나). 선형 개방 주소 지정법의 장단점
- 장점 : 해쉬 테이블의 구조가 간단 , 구현단순
- 단점 : 충돌이 발생한 경우에, 최악의 경우 해쉬 테이블 전체를 검색해야 하는 경우가 발생
- 불필요한 Bucket 을 탐색 이미 사용된 Bucket 을 처음부터 탐색
- 적재율이 낮거나 Record 들의 개수를 미리 예측 가능할 때 사용
다) 체인 이용법
- 충돌이 발생한 경우에 동일 버켓에 들어가야 할 명칭들을 연결 리스트로 저장해 두는 방법.
- 체인 이용법을 이용할 때는 해쉬 테이블의 각 버켓이 하나의 연결 리스트가 된다.
-같은 데이터 주소 내에서 끝까지 해결하는 방법
-같은 해시 값을 가지는 모든 레코드들을 list 로만들어 관리
라) 체인 이용법의 장단점
- 장점
. 충돌이 발생한 명칭들만을 연결 리스트에서 검색해 주면 되므로 속도가 빠르다.
. 삽입 가능한 명칭의 수가 해쉬 테이블 크기에 영향을 받지 않는다.
. Overflow된 bucket에 관련된 Record들만 검색 .
. Record 개수를 미리 예측하지 못할 때 사용
- 단점
. 구조가 복잡하고, 기억장소 소모량이 많다.
. Link Space Overhead 를 위한 발생 .
Ⅳ. Hashing 적용 분야
해슁을 사용하면 검색 시간이 어느 한도 내에서 보장되므로, 검색 시간이 비용과 직접적으로 연결되는 분야에 이용하도록 해야 한다. 신용 조회, 이동 통신, 카드 결제 등과 같은 실시간 통신은 일정한 검색 시간이 무엇보다도 중요하다. 따라서 이런 분야에서는 실제적으로 해슁을 이용한 데이타베이스로 운용을 해 나가고 있다.
해슁의 단점은 연속적인 데이터의 검색이 비효율적이다라는 것이므로 연속적인 질문을 던지는 데이타베이스에서는 사용하지 않는 것이 현명한 처사이다.
※ Hashed File
- 직접 파일(Direct access method : DAM 또는 Random access method : RAM)이라고도 함.
-해싱 기법을 이용하여 레코드에 액세스할 때 주소를 직접 사용자가 지정하는 방식의 파일로서
레코드의 처리는 키 항목에 따라 랜덤 처리하는 것을 기본으로 함.
※. Hash Join
- DBMS 에서 Join 을 처리할 때 해시함수 적용을 통해 대량의 데이터를 보다 효율적으로 Join 함.
※. Hash Partition
- DBMS 에서 대량의 테이블을 해시함수를 적용하여 파티션으로 나눔으로써 파티션에 데이터가
균등하게 배분되도록 유도함
'C.E > File processing' 카테고리의 다른 글
| DBMS에서 사용하는 B+ Tree (0) | 2014.06.10 |
|---|---|
| 해쉬 테이블 (해시 테이블/hash table) 완전정복+(Java) (0) | 2014.06.05 |
| B+ 트리 (0) | 2014.06.05 |
| B트리 (0) | 2014.06.05 |
| C++ 합병정렬 소스(merge sort in have data) (0) | 2014.05.20 |